私大医学部の過去問を見ていきます。
今回は、2021年日本大学の前期数学・A方式。
日大は昨年まではA方式(個別)とN方式(全学部共通試験)の2つの日程がありました。A方式の定員が97名、N方式の定員は10名なので、A方式の方がメインでした。
次からは、N方式のみとなります。ただし、全学部共通問題のほかに2次試験で英語・数学が実施されます。この2次試験が今までのA方式のような問題ではないか、と予想されます。
数学についていえば、昨年までのA方式は75分間で大問5問。うち2つが小問集合でマーク式、1つがマーク式大問、そして残り2つが完全記述式(途中経過も記述)大問、という構成でした。
2022年の数学2次試験は、60分間・記述式で実施することが発表されています。おそらくいままでのA方式で出題されていた小問集合は、あまり出題されないと思われます(1次試験(全学部共通試験)のほうに任せる)。
時間の比率を考慮すると、2022年の数学2次試験は、大問4問出題が予想されます。しかしこれについては、実際にどうなるかは分かりません。
[4] (3)数学IIの微積分です。3次関数の一部分の面積を出して、接線の式を出す、というものです。解き方もシンプルです。ですが計算は煩雑です。
こういう問題は少し悩みます。簡単な解き方があるのではないかと、ふと思うんですね。これは過去問を解いて「相場」を身につける必要があります。予備知識なしで問題を解いていると、途中式が複雑になると少し不安になりますが、「この大学はある程度の計算量が要求される」と知っていれば安心して解き進められます。
そして、この分野は特に計算量が大きくなるところだということも、知っておくと安心です。センター試験でも、積分計算が意外と繁雑だったことがありました。
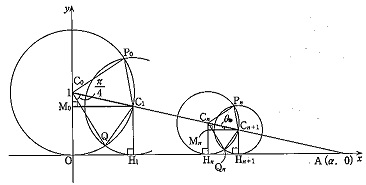
[5] 図形と無限等比級数。(2)(3)の計算が特に大変です。(2)まで解ければ十分だと思います。
ただ、完全記述の問題なので、不十分な記述で減点されることに注意です。2次方程式の解のうち一つを採用して話を進めるときや、文字で割るときなどに、適切な断り書きを入れるクセをつけておきましょう。
(3)は、隣りどうしの円の重複部分の和を求めるものです。扇側の面積と三角形の面積の差を出します。なんだか中学入試の算数みたいな図形の形ですが(解き方は似ている)、計算が大変です。試験本番でも、解かなくていいと思います。これに手を出す時間があるなら、小問集合の検算をしたほうがいいでしょう。
対策です。
まずは、取れる問題を取ることです。そして数学では、取れる問題かどうかはある程度解き進めてみないとわからないことが多いので、見極める力が大切になります。たとえば三角形の問題がでてきたら、三角比、ベクトル、初等幾何、と素早くいろいろ進めてみて突破口を探すという感じです。最初に思い付いた解き方が実はものすごく効率が悪い解き方だった、ということもあるので、1問あたりの解答時間に制限時間を設定して進めていくことも大切です。
そして普段の勉強では、完全記述型の答案作成を意識する必要があります。多くの私大医学部はマーク式または最終解答のみ記述というものが多いので、それに照準を合わせた勉強法ばかりだと、途中経過については大雑把になってしまうことがあります。
これについては、普段の記述模試がいいトレーニングになります。河合塾の全統と比べると、日大A方式の方が問題のヒネリは少ないですが、その割には計算量が多いです。模試の採点をよく読み直して、自分の答案の記述の甘さをチェックするとよいでしょう。文字を置いた時の範囲の明示などは、クセをつけておきたいところです。